Paper URL: https://arxiv.org/pdf/2503.01776
Code URL: https://github.com/neilwen987/CSR_Adaptive_RepConference: ICML’25 Oral
TL;DR
This paper introduces CSR, an effective learning method for sparse adaptive representations. It combines a task-specific sparse contrastive learning loss with a reconstructive loss to maintain overall embedding quality.
Intro
MRL, as an existing method to compress representations, truncates the linear layers into a set of target sizes to reflect representations of various dimensions.
However, MRL faces two key constraints:
- it requires (full) training of the backbone parameters;
- its performance often deteriorates a lot under small hidden dimensions.
Method
CSR combines sparse contrastive learning and sparse autoencoding to maintain overall embedding quality.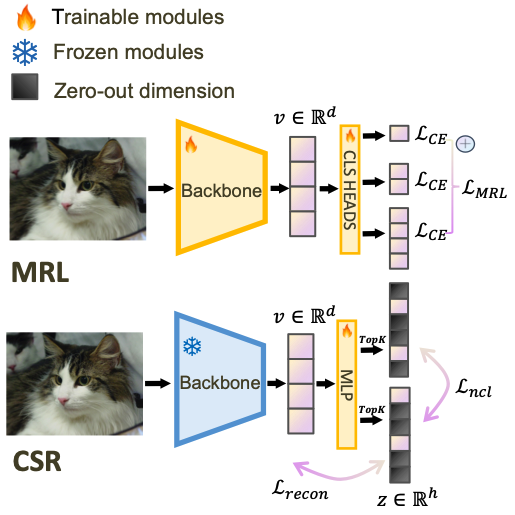
Sparse Autoencoders(SAEs)
SAEs aim to extract a sparse representation $z_k$ by learning to reconstruct the dense feature from $z_k$.
Denote the (weights, bias) of encoder and decoder as $(W_{enc},b_{enc})$ and $(W_{dec},b_{pre})$. And $f(x)$ represents the dense feature of input $x$.
Encoding
$\text{TopK}$ gets $K$ largest values. $\sigma^+(\cdot)=max(0,\cdot)$ is the ReLU activation.
This process encodes the dense representations into sparse representations, with only $K$ non-zero values.
Decoding
This process decodes and reconstructs the original embedding using sparse representation $z_k$. To make $\widehat{f(x)_k}$ as similar to $f(x)$ as possible, it uses L2 reconstruction loss as the main training objective:
Dead Latents
As the large number of zeros in sparse representations, a lot of latent dimensions remain inactive during training - a phenomenon called the Dead Latents. This is one of the reasons of the performance degradation.
To mitigate this issue, an auxiliary loss $\mathcal{L}_{aux}$ and Multi-TopK losses are proposed.
Auxiliary Loss
where $e=f(x)-\widehat{f(x)}$, and $\hat{e}=W_{dec}z$. This is the forced reconstruction using the top-$k_{aux}$ dead latents.
Multi-TopK Losses
An extra $4k$ reconstruction is added.
The overall construction loss is
Sparse Contrastive Learning
Simply reconstruction is not enough to make sparse representations distinguishable. So contrastive learning is introduced to enhance the semantic discriminative power of sparse representations.
Supposing batch size $\mathcal{B}$. $z_i$ represents the $i$-th sample in the batch. The contrastive loss is defined as
This makes each latent representations closer to the positive samples (itself) and further to the negative samples (other representations).
Notice that all the $z$ are non-negative by $\text{ReLU} + \text{TopK}$ selection, thus this contrastive loss is a variant of the Non-negative Contrastive Loss (NCL).
Theorem 5. Under mild conditions, the solution $\phi(x)$ is the unique solution to the NCL objective. As a result, NCL features are identifiable and disentangled.
According to the above theorem, the sparse contrastive loss tends to relate each latent dimension to a specific stable and distinguishable semantic factor. It also helps mitigate the dead latents issue.